Mass-spring systems are often used to model the behavior of an isolated vibrating system.
The mass-spring viewpoint should not be utilized in cases where the system can not be reliably modeled as a mass-spring system. The importance of the static compression of the isolating material, due to gravity, is also overemphasized and often misunderstood.
Some important points:
- The mass isolates vibrations by resisting change of momentum. Usually: the more mass, the better. The weight (due to gravity) has very little to do with the isolation, it’s the mass that matters!
- The spring’s main purpose is to carry static forces (for example the weight). It will also try to resist the displacements of the mass, which means that it will transfer forces to the foundations. From the perspective of isolating vibrations, the spring should be as loose as possible, to allow for the mass to vibrate freely.
- The mass-spring combination only works on frequencies higher than the resonance frequency.
- Ideally, there would be no “spring”, but it’s impossible in practice.
Simplifying rotating parts
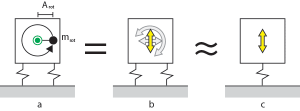
Let’s start from the very basic reasoning behind why the mass-spring perspective is so common when designing vibration isolation. Consider case a. We have a machine, with a part rotating around some axis.
Case b shows the varying forces such a movement creates. Perpendicular forces exist relative to the x-axis and y-axis. The varying force in the direction of the x-axis, together with the resisting force at the support, also create a moment of force (kind of like attempting to tip the machine over). The vertical component of the force often creates a moment of force, as well. As does accelerating or decelerating angular motion.
In practical cases, it has been shown that it’s often enough to consider the sinusoidal force shown in case c (but it’s not always enough!).
Note that this model assumes both the machine and the support to be perfectly rigid. Note also that the force required to keep the rotating mass in bay will rise along with the frequency ($$\omega^2$$)! I think I will return to this in another post.
The equilibrium of the system
So far we have simplified the system to a sinusoidally varying vertical force, acting on a mass on a spring.
We will describe the system using these parameters:
- The mass of the machine
- A varying force directed on the machine
- The varying displacement of the machine
- The spring constant, which we’ll assume to be constant (linearly elastic)
We now have five different sources for forces:
- $$F_{m} = ma = m\ddot y$$, caused by the mass/momentum of the machine which resists acceleration
- $$F_{k} = k y$$, caused by the compression of the spring
- $$F_{c} = cv = c\dot y$$, caused by various energy losses which are directly proportional to the speed of the displacement
- $$F_{e}$$, external forces which we feed into the system.
- $$F_{g}$$, the force of gravity pulling down the mass
Using the principle of equilibrium (Newton), the sum of these forces must be 0.
$$F_k + F_c + F_m + F_e + F_g = 0$$
$$F_g$$ can be discarded in our calculations. I’ll soon explain why.
Calculating the natural frequency of the system
We know that such a system oscillates naturally at a specific frequency. To calculate this frequency, we assume three things:
- The motion is sinusoidal
- There are no external forces ($$F_e$$)
- The damping factor ($$F_c$$) approaches zero, allowing for the system to oscillate freely
By assuming the motion follows the function $$y(t) = A\sin(\omega t)$$, we get the following equation:
$$F_k + F_m + F_g = k(y(t) + y_0) + m\ddot y(t) + mg = k A\sin(\omega t) – m A \omega^2\sin(\omega t) = 0$$,
where $$y_0$$ is the compression caused by the pull of gravity.
$$k y_0$$ has to be equal to $$m g$$ for the system to balance out (Hooke’s law), which means that we can throw the effect of gravity out of the equation. Intuitively this can be explained as following: as the effects of gravity and the static compression of the string ($$k y_0$$) constantly cancel each other out, only the vibrating part of the displacement ($$y(t)$$) makes any difference. The force caused by the vibrating part of the displacement is still directly proportional to the spring constant. Gravity (and as such the static compression of the spring) makes no difference. Gravity only affects the situation if the spring constant changes because of it, not because it compresses the spring or adds a constant downward force to the mass. This holds true for all constant forces, so constant forces should never be included in a vibrating mass-spring system to avoid confusion! They should only be used to calculate the correct spring stiffness, which is almost always very nearly linear when the vibrations are small.
The forces will balance out when $$\omega = \sqrt{\frac{k}{m}}$$, or $$f_0 = \frac{1}{2 \pi}\sqrt{\frac{k}{m}}$$.
Note that this is the combined natural frequency of the spring and the mass! This might seem obvious now, but when we replace the mass and spring constant with something else, it might not be that obvious. The compression of the spring, using Hooke’s law, will be $$mg = k\delta x$$. Inserting this into the formula will give $$f_0 = \frac{1}{2 \pi}\sqrt{\frac{g}{\delta x}}$$. This formula is often used for practical purposes, but effectively hides the real parameters the natural frequency is based on!
Calculating the forced response of an undamped system
We will consider the steady state response, meaning the response of the system after being excited at a specific frequency for a long time (when everything balances out). We will assume the mass will move at the same frequency as the force exciting it.
The equilibrium formula shown earlier will now look like this:
$$m \ddot y(t) + k y(t) = F(t)$$
Assuming the machine will be excited according to the function $$F(t) = F\sin(\omega t)$$ (ignoring everything else for now) and the machine moving according to the function $$y(t) = A\sin(\omega t)$$ we get the following formula:
$$-m A \omega^2 sin(\omega t) + k A sin(\omega t) = F_0\sin(\omega t)$$
Solving for A (the amplitude of the motion caused by the force), we get the following formula:
$$A = \frac{F_0}{-m \omega^2 + k}$$
Note that this describes the displacement of the mass. I think the following concept is really important to understand; the force transmitted into the foundations is directly proportional to the displacement. As the spring constant approaches zero (let’s imagine the mass floats in space, for example), the system will still vibrate with an amplitude of $$\frac{F_0}{m \omega^2}$$. Increasing the mass will decrease the amplitude of the vibration, also when there is no spring.
To get the force transmitted into the foundations of the machine, we need to multiply the displacement with the spring constant $$k$$ (according to Hooke’s law). From this, we get the relation of the transmitted force to the original force $$\frac{F_{tr}}{F_0}$$:
$$\frac{F_{tr}}{F_0} = \bigg\vert\frac{1}{\frac{-m}{k}\omega^2 + 1}\bigg\vert$$
The formula nicely shows us a few things:
- The resonant frequency is at $$\omega = \sqrt{\frac{k}{m}}$$, which is the same as earlier
- The effect of decreasing the stiffness of the spring
- The effect of increasing the mass of the machine
Thoughts
Please note that this has been a significant simplification of the situation. Ideally, the simplification only works for cases where the vibrating force is purely vertical, and acts in the exact direction of the centre of mass of the object.